STORIA DEI NUMERI. Quegli strani modi in cui gli Antichi scrivevano le cifre.

LE CIFRE DEL MISTERO

MA COME SCRIVEVANO I NUMERI, GLI ANTICHI?

Sembrava che si sapesse già tutto dell’origine grafica della nostra numerazione, eppure si continuano a scoprire documenti e studi del passato da cui emergono strani sistemi di cifre, a metà tra matematica e magia. Il risultato? Si allontana la tesi “araba” e si avvicina l’ipotesi europea, greca o caldea.

NICO VALERIO
Scienza 2000, luglio 1986 (revisione con aggiunte: 2001)

La matematica non è un'opinione. Eppure non c'è nulla di più mutevole, incerto e impreciso della rappresentazione grafica dei numeri. Anzi, a ripercorrere all'indietro la storia della numerazione, sembrerebbe proprio che un sistema numerico scritto non sia nient'altro che un codice linguistico come un altro, un’opinabile convenzione.
      La varietà della scrittura numerica, certo, lascia sbalorditi, e smentisce quello che il matematico tedesco Leopold Kronecker, vissuto nell’Ottocento, andava ripetendo: «Dio creò i numeri, tutto il resto è opera dell'uomo», come per dire che non conviene indagare troppo sulla natura dei numeri o sull’origine della loro scrittura. Al contrario, è vero, semmai, che prima nascono le cose, la Natura, e poi gli Umani si mettono d’accordo per inventare i numeri, cioè per contare le cose, gli uomini stessi, gli animali, gli eventi. Ma i sistemi grafici numerici sono stati così numerosi, mutevoli e alle volte ammantati di mistero, che eruditi e matematici, che pure erano d'accordo sulle leggi dei numeri, si sono spesso confusi o hanno litigato sulla loro grafia.
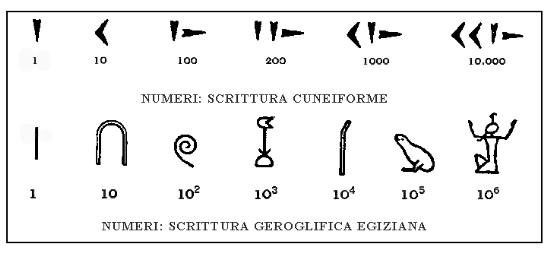      Prima che la diffusione della scienza sperimentale e della cultura portasse ovunque i cosiddetti numeri “arabi” – vedremo in seguito quanto imprecisa o errata sia questa definizione – si può dire che ogni civiltà degna di questo nome abbia adottato un proprio particolare codice numerico, con tanto di differenziazione grafica. Il risultato? Una vera e propria Babele di segni di quantità, così diversi tra loro da far pensare al pluralismo caotico degli alfabeti, piuttosto che alla razionalità unificante della matematica. E poiché molti di tali sistemi hanno una chiara derivazione alfabetica, non dobbiamo meravigliarci se in un sistema di numeri scritti o disegnati si mescolano in un tutt'uno esigenze di razionalità e rappresentazione del mondo reale (per es. nella scrittura numerica geroglifica, egiziana o proto-cinese), praticità di calcolo e simboli magici, misterici o religiosi.

Che i segni per rappresentare i numeri non dovessero essere troppo diversi da quelli delle parole, spesso i medesimi con qualche variante, è una costante che accomuna i popoli dell’Antichità remota, dai Mesopotamici agli Egizi, dai Cinesi agli Ebrei, dai Greci agli Etruschi.

I numeri latini sono ancora tra noi, oltreché nei libri di storia (genealogie e nomi di re), usati ormai solo per occasioni solenni o festività ufficiali. Nessuno scambia il II capitolo d’un libro per l’undicesimo, anche perché viene dopo il I e prima del III. Il XX Settembre è la ricorrenza di Porta Pia, cioè dell’ingresso degli Italiani a Roma (e c’è anche la via), anche se c’è qualcuno che scrive 20 Settembre. Il XXI Aprile è la leggendaria data della fondazione di Roma (e a Roma c’è una via). Neanche i papi Giovanni XXIII e Paolo VI danno problemi. Insomma, le regole dei numeri latini più semplici sono risapute.

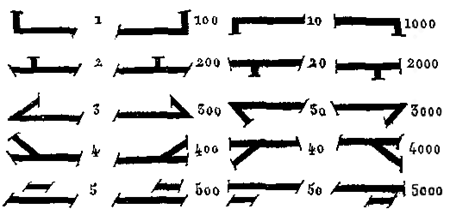
A Roma, per l’influenza dei vicini Etruschi, che del resto furono classe dirigente e perfino regnante nel periodo dei Re, si usò un sistema molto simile alla numerazione etrusca, partendo dalle arcaiche lettere dell’alfabeto. Confrontando la grafia etrusca e quella latina classica, a noi più familiare, dobbiamo ovviamente considerare che gli Etruschi scrivevano da destra a sinistra. Anche a Roma, il segno elementare di un dito, quella che poi fu codificato curiosamente come la lettera i maiuscola, stava per il numero uno. Due dita, ovvero II, per il nostro 2, III per 3, IIII o IV per 4 (nel Medioevo solo IV). L’evidente segno del palmo della mano, quindi comprendente 5 dita, quella che poi fu codificata come lettera V, sta per 5. Intuitivamente altre “dita” si possono aggiungere alla “mano”. E dunque VI è 6, VII è 7, VIII è 8. Il 10 altro non è che due mani, cioè dieci dita, a cui si possono sottrarre o aggiungere altre dita: IX sta per 9, XI per 11, XII per 12, ecc. Altre cifre tonde sono per la numerazione latina L che per 50, C per 100, D per 500, M per 1000 (che in certe epigrafi a scrittura “unciale” è scritto CIƆ). Gli accostamenti tra lettere seguivano la regola “additiva” (più lettere accostate si sommano), ma anche la regola sottrattiva e moltiplicativa. Per operazioni matematiche complesse, anche quella esponenziale.
      Già gli Etruschi avevano indicato ai Romani il binomio di sistema additivo e sottrattivo, e alcuni simboli più complessi. La lettera V per gli Etruschi era una “mano” rovesciata in basso, come una lambda greca, mentre per i Romani la mano è rivolta verso l’alto. Come si vede dalla tabella, però, nel caso di numeri composti da più lettere bisogna considerare che la scrittura etrusca, a differenza di quella latina classica, procede da destra a sinistra.
      Ecco qualche esempio di scrittura additiva dei Romani. L’anno 2000 i Romani lo avrebbero scritto MM, 2005 semplicemente MMV. Se a Roma un candidato riportava 3407 voti, questo numero lo si scriveva MMMCCCCVII, come addizione di 1000 + 1000 + I000 + I00 + 100 + 100 + 100 + 5 + I + I. Ma per un’altra regola, additiva-moltiplicativa, lo stesso numero si poteva anche scrivere IIIMIIIICVII, cioè 3 x 1000 + 4 x 100 + 7. Un numero, così, finisce per essere una “somma di moltiplicazioni”.
      E la regola sottrattiva? Quando una lettera è seguita da una lettera di valore più alto, si deve seguire la regola sottrattiva cioè il “principio di differenza” tra i due valori. IV vale 1 che va sottratto a 5, ovvero 4. Allo stesso modo IX = 9, cioè 10 meno 1, XL = 40, XC = 90, CD = 400, CM = 900. Ma nella Roma antica 4 era quasi sempre segnato come IIII (e perciò troviamo perfino su qualche quadrante di orologio meccanico moderno le ore 4 segnate come IIII). Solo nel latino medioevale il IV divenne tassativo.
      C’è anche una certa elasticità nel sistema di scrittura delle cifre latine. Tanto che l’anno della scoperta dell’America (1492) gli scalpellini del Papa potevano inciderlo in un’epigrafe come MCCCCXCII, e in un’altra - più brevemente - come MCDXCII.
      Per rapidità stenografica o per ragioni di spazio (era il caso degli scolari a scuola, dei commercianti e degli scalpellini sulle epigrafi) le moltiplicazioni per 1000, 100.000 e 1.000.000 erano semplificate da un simbolo grafico. Una lettera (p.es. V o X o C) se sormontata da una sola lineetta si intendeva moltiplicata per 1000, se alla lineetta si aggiungevano due lineette laterali – insomma un ponte – si doveva intendere moltiplicata per 100.000, se invece era sovrastata da due lineette parallele si intendeva moltiplicata per “mille migliaia” (i Romani come tutti gli Antichi non calcolavano il milione: ragionavano a migliaia).
      Scritture di tipo additivo sono state usate dagli Egiziani nella notazione geroglifica, dagli antichi Semiti, dagli Indiani, dai Greci, dai popoli italici. La scrittura cuneiforme (vedi figura) usava il sistema moltiplicativo. La scrittura di tipo esponenziale prende come esponente anziché come fattore il numero delle volte che una data unità d'ordine superiore deve essere calcolata. I due sistemi si trovano usati anche in modo misto. Casi di scritture di tipo esponenziale abbondano specialmente presso i popoli dell'estremo Oriente, come Cinesi e Giapponesi.

LE LETTERE-NUMERI: LA SCRITTURA DEI GRECI
Immaginiamo che complicazione scrivere a quei tempi una semplice sottrazione come 3.542.796 meno 1.008.174. C'è ragione di ritenere che nel calcolo corrente si preferissero sistemi più rapidi e abbreviati, ricorrendo anche ad indici di moltiplicazione, come si deduce anche dalle epigrafi e dalle iscrizioni monumentali. Per esempio, una M chiusa in un circolo o tra due parentesi tonde, come (M), aveva un valore dieci volte maggiore, cioè 10.000. Insomma, una specie di “stenografia” numerica.I Greci usavano come cifre i ventiquattro segni del loro alfabeto muniti di un apostrofo (in realtà era uno iota, cioè una piccola i) a destra in alto. Le lettere-cifre erano divise in tre parti: unità, decine, centinaia. Per indicare le migliaia, le decine di migliaia e le centinaia di migliaia, i Greci usavano le stesse lettere con l’apostrofo in basso a sinistra. Con questo sistema, essi potevano esprimere i numeri fino a 999. Per es.: 257 = snz’ oppure 386 = tpς’ ecc. Così, per es., 80.000 è rappresenta­to, al pari di 80, da pi-greco (p) ma con l'apice a sinistra in basso: ,p. Talvolta le lettere in uso non bastavano e si  ripristinavano lettere antiche. Al 6°, al 18° e all'ultimo posto, ad esempio, i Greci aggiunsero tre segni grafici del tutto nuovi, solo numerici, il sampi, il coppa e il vau, che valevano 6, 90 e 900 (più i loro multipli). Cifre che sono poco note al largo pubblico, e perfino a qualche lettore di buona cultura classica. In questo modo era possibile arrivare fino a 999.999. Che si scriveva:

Ma si usavano anche alcune varianti. Per esempio, il 90 era rappresentato anche come un cerchio un po’ più grande della O, segnato da un trattino ortogonale in basso, quasi come una maiuscola Q o una O con un puntino in basso: Ọ, come mi ricorda l’epigrafista romano Nicolò Brancato.
      Addizioni, sottrazioni e moltiplicazioni erano eseguite in modo molto simile al nostro, anche se con maggior scomodità. Il numero 2001, p.es., nell’Atene di Pericle sarebbe stato rappresentato graficamente con due lettere dell’alfabeto diversamente accentate: ,ba’.

E PER IL COMMERCIO E LA STENOGRAFIA? LE “FIGURE D’ABACO”. Quando iniziò a modernizzarsi il nostro sistema di scrittura numerica e a divenire più pratico e veloce? Nella numerazione moderna, com’è noto, lo stesso segno può avere valori diversi a seconda della sua posizione. Lo zero, poi, a differenza che nel mondo greco-latino, è rappresentato. Cosicché esiste una grande differenza tra 35 e 350, nonostante che i singoli valori numerici siano i medesimi.
      La tesi finora più ripetuta è che questa razionalizzazione della numerazione fondata sul valore di posizione sia stata iniziata dagli Arabi, anche se alcuni indizi storici potrebbero in realtà farci risalire alla lontana India. Secondo questa ipotesi, comunque, dalla lontana penisola indiana agli Arabi, intorno all' VIII sec. d.C., e dagli Arabi alla Spagna nel sec.XIII, e poi in tutta Europa, la numerazione oggi definita semplicisticamente «araba» avrebbe acquistato subito i suoi grafismi originali, analoghi a quelli arabi moderni; e si sarebbe diffusa in una forma occidentale ingentilita (cifre ghubàr) che riecheggiava più direttamente i numeri índiani o le loro deformazioni invalse nell'uso europeo. Lo zero avendo una grande importanza nel nuovo sistema, specialmente per semplificare i conti del commercio, dal XV secolo i numeri cominciarono ad esser chiamati «cifre» (da sifr, nome arabo dello zero, confronta con. l'inglese cipher, che sta tuttora per zero). Questa è la “vulgata” accettata tradizionalmente.

      In realtà, le cose non stanno proprio così. Innanzitutto, sull'adozione delle cifre attualmente diffuse in tutto il mondo, è accertata l'influenza determinante della profonda cultura matematica europea, a cominciare dal movimento di Pitagora e poi dei neopitagorici. E non è pensabile che la potente civiltà di Roma, che allora dominava il mondo nei commerci e nella tecnica più degli Stati Uniti d’America oggi, non avesse sviluppato un sistema pratico e veloce di scrittura dei numeri. Sembra, infatti, che i Romani già nell'abaco, cioè nel primo grado del far di conto, e nel computo commerciale, avessero nozioni precise dei cambiamenti di valore d'una cifra a seconda della sua posizione. Fatto sta che per secoli, fino al Medioevo, la scuola e la pratica di bottega avevano reso popolare tale sistema di numerazione, noto come “figure d’abaco”, gli "apici" di cui parla una nota probabilmente apocrifa del trattato Geometria di Boezio. Tanto che quando Guido d'Arezzo, nel suo Trattato sul computo, e soprattutto Leonardo Fibonacci, nel suo Liber abbaci (1202), codificarono il sistema posizionale utilizzando le cosiddette cifre “arabe”, si può ritenere che l'Europa fosse già preparata da tempo alla novità.
      Ma, ecco il punto, quali figure numeriche erano usate in Italia nell’Alto Medioevo? Non certo le figure arabe, che pure iniziavano a diffondersi nel vicino Oriente, ma figure di probabile provenienza indiana, che pare fossero usate nella pratica commerciale già dai Romani. Ed è davvero singolare la somiglianza esistente tra queste antiche grafie numeriche e quella attualmente in uso nella civiltà occidentale, erroneamente denominata “araba”:

Certo, a noi moderni anche i nomi di queste strane figure di numeri, dall'1 al 9, sembrano insieme esotici ed esoterici: Igin, Andras, Ormis, Arbas, Quimas, Calcus, Zenis, Temenias, Celentis. Le forme per noi più misteriose, probabilmente residui di antichi significati alchemici o magici, sono quelle che si intravvedono nelle figure di Ormis e Arbas (equivalenti al 3 e al 4). Però, ad osservare attentamente le singole figure, cogliamo impressionanti somiglianze con i nostri numeri in ben sette numeri su dieci (1, 2, 3, 6, 7, 8 e 9) e una più vaga somiglianza nel numero 5. Scrivendo un numero a caso, per esempio il 6891, in forme di figure d’abaco, otteniamo cioè una figura molto simile, certo molto più simile dell’equivalente numero arabo reale,  , scritto da destra a sinistra. Ma anche se fosse scritto da sinistra a destra, a noi occidentali moderni direbbe ben poco: .
      Nonostante quello che si usa ripetere, quindi, la grafia “araba”, se non improbabile, appare almeno molto lontana, e comunque mescolata ad altre culture. Ma quali? Una tavola di confronto tra vari documenti pervenuti dal Medioevo lascia meravigliati per la curiosa persistenza delle forme dei simboli numerici usati nell'abaco dal 900 dC al XIII sec. praticamente senza evoluzione. Il che lascia perplessi.

Gli elementi misterici e magici, erano intrinseci alla numerologia antica. Nella cultura europea, basta citare tutte le Scuole di Pitagora. Circostanza questa che deve aver influito senza dubbio anche sull'invenzione grafica delle singole cifre, in ragione di quella rappresentatività simbolica che è alla base della numerazione antica. Così accanto ai sistemi di numerazione correnti, diremmo laici o commerciali o scolastici, ogni epoca contava numerosi altri sistemi di numerazione paralleli, diremmo esoterici o eruditi o addirittura segreti (crittografici).

MAGHI, ERUDITI E AVVENTURIERI ALLA RICERCA DEI NUMERI DEL MISTERO.  Dal Rinascimento fino a tutto l'800, affascinati dal mistero del numero, sapienti appartenenti ad ambienti sacerdotali, varie categorie di eruditi (maghi, pensatori, guaritori, erboristi, alchimisti) e certamente gli umanisti, gli studiosi ebrei di “kabbalah”, i letterati esperti di sanscrito e greco antico, si dilettarono nell’andare a ritroso alla ricerca dell’origine della scrittura numerica. Finirono, così, per riscoprire e rimettere in voga antiche e desuete numerazioni, sistemi ormai sepolti e dimenticati di rappresentazioni matematiche, codici contenenti cifre misteriose tutte da interpretare. L'Oriente, ancora una volta, fu il grande deposito a portata di mano dove attingere tutte le scoperte. Antichi Sumeri e Mesopotamici, proto-Egizi e Indiani, Cinesi antichi e moderni, Ebrei prima e dopo la diàspora, furono naturalmente al centro della morbosa attenzione di questi avventurosi «cercatori di cifre», eclettici per cultura e disinvolti come filosofi sincretistici.

      Proprio di uno di tali eccentrici eruditi innamorati dei numeri antichi e misterici abbiamo trovato traccia in una rara raccolta scientifica francese uscita a dispense alla metà dell'800. Quella che emerge è proprio la figura d'un tipico uomo di cultura del Medioevo, al quale si richiedeva di essere esperto nel “trivio” e nel “quadrivio”, versato cioè nelle artes sermocinales, utili alla parola, e nelle artes reales, indispensabili alla conoscenza del mondo esterno. Le prime erano grammatica, dialettica e retorica; le seconde erano aritmetica, geometria, astronomia e musica. Ma un vero uomo di cultura dell'epoca sapeva di più, molto di più.
      Giovanni di Basingestokes, arcidiacono di Leicester, era uno di questi. La sua cultura ‑ tramandano i contemporanei – spaziava in tutti i campi dello scibile, la sua erudizione comprendeva l'alchimia e la numerologia, senza contare ovviamente le lingue: greco, ebraico e latino. Che sappiamo di lui? Poco o nulla, ma quanto basta per incuriosirci. L'erudito monaco benedettino inglese Matthieu Paris(1200-1259) racconta nella sua «Grande cronaca» (Historia maior Anglorum) che, verso l'anno 1252 il signore di Basingestokes, passò a miglior vita. Nella traduzione francese dell'800 (a cura di Huillard-Bréholles), citata nella curiosa raccolta da noi ritrovata, alle pagine 319 e 320 del Magasin pittoresque (anno1850; redazione a Parigi, in rue Jacob, n.30), il maestro Giovanni è descritto ‑ ecco il punto che ci interessa ‑ come colui che «aveva portato in Inghilterra le antiche figure numerali dei Greci», le aveva fatte conoscere ad amici e discepoli, le aveva interpretate». Sennonché le cifre «scoperte» dal colto inglese appaiono subito troppo primordiali per essere attribuibili alla numerazione greca. Sembrano di origine ancor più orientale e antica.

CIFRE “SEGRETE” DI ORIGINE CALDEA USATE DAI GRECI?Nello stesso titolo l'anonimo redattore francese del 1850 avanza l'ipotesi che le singolari cifre siano appartenute alla tradizione dei Caldei. A meno che un simile tipo di grafia numerica non fosse destinato in Occidente ad un uso «parallelo» e non ufficiale, in qualche modo legato a riti e funzioni misteriche. E' possibile, cioè, che gli antichi eruditi dell'area mediterranea, e quindi anche eruditi e astrologi greci, utilizzassero in certi casi a scopo criptico numerì e sistemi numerici di provenienza orientale, in sostituzione del sistema corrente.Ecco qui sopra, nel loro segno tipografico impreciso e sbavato di 150 anni fa, così come li abbiamo trovati nella polverosa rivista francese dell’800, i singolari segni attribuiti ai Greci dalla cronaca del monaco Matthieu.
      E' lo stesso antico cronista a far notare che tutti questi caratteri derivano da un tipo unico, ossia da un segno cuneiforme verticale con cui altre linee formano angoli acuti, retti e ottusi; e che tutti i simboli di unità sono formati da una verticale e da linee tirate da destra a sinistra, mentre i simboli delle decine sono ottenuti dalla medesima verticale e da linee tirate da sinistra a destra.
      Questo passaggio di Matthieu Paris ha indotto in errore l'umanista Fabricius, l'abate Leboeuf, gli storici della letteratura Benedettini compresi ‑ e molti altri scrittori, che attribuiscono a Giovanni di Basingestokes il merito dì aver introdotto in Occidente le figure delle cifre greche. A chiarire l'equivoco è stato lo studioso Charles Jourdain che, in una conferenza sullo stato della filosofia naturale nel XII secolo, tenuta nel 1838, fece notare che già il Trattato dell'analisi dei numeri ‑ opera certamente scritta dal 1147 al 1149 ‑ racchiude una menzione formale delle cifre greche e una tavola molto esatta dell'uso aritmetico delle lettere dell'alfabeto greco.
      Sicuramente le lettere, come si è detto, servivano anche da cifre per i commercianti, i matematici e, gli studenti, greci; ma lo Jourdain precisa che, inspiegabilmente, solo le lettere-cifre C, D, L, V, I e X erano d'uso generale, essendo l'impiego delle altre «più raro». Che cosa vuol dire? Non è chiaro. Quel che è certo, comunque, è che l'introduzione delle cifre greche in Occidente risale a un'epoca molto più antica di quanto si immagini comunemente: almeno quattro secoli prima dell'ìntroduzione della numerazione latina-romana.

ALFABETI SCOMPARSI E ALFABETI SEGRETI. Ed anche i popoli che avevano contatti commerciali con Greci e Romani, adottarono la loro scrittura numerica, con alcuni adattamenti. Come ha riferito il “venerabile” Beda, Dottore della Chiesa e forse il maggior erudito dell'Alto Medioevo, l'umanista Giovanni Tritemio nella sua misteriosa opera Polygraphia raccolse documenti eccezionali su tutti gli alfabeti segreti e scomparsi, su tutte le scritture numeriche, perfino quelle magiche ed esoteriche. E proprio da quest'opera, grazie ad alcune testimonianze di eruditi del passato, apprendiamo che i Normanni, all'epoca della loro scoperta della Gallia, avevano adottato un sistema numerico misto, adattando il sistema greco alle lettere latine di cui allora essi si servivano. In tal modo riuscivano a scrivere i primi ventiquattro numeri:

Riportiamo queste figure numeriche da un'antica edizione della Polygraphia (Colonia 1564, in‑8) riprodotta nella raccolta francese che abbiamo ritrovato, e riferiamo che secondo lo studioso dell’800 esistono singolari ed inquietanti somiglianze tra queste figure e gli «apici» raffigurati da Boezio, il celebre poligrafo latino. Quello che balza agli occhi è che, a parte le anomalie dei numeri 10 e 20, tutti i numeri di due cifre sono scritti secondo il nostro attuale sistema di numerazione, dando un valore di posizione alle cifre che rappresentano le decine.

      L'analogia, comunque, resta ed è tale da rafforzare l'opinione di alcuni studiosi antichi, secondo i quali il nostro attuale sistema di numerazione, impropriamente attribuito agli Arabi, ha in realtà origine occidentale o, per lo meno, è stato mediato e trasmesso a noi dai Greci e dai Caldei. Matthieu Pâris, dunque, ha preso un abbaglio, ed ha confuso con le vere cifre greche il particolare sistema riportato dall'arcidiacono di Leicester, sistema di cui nondimeno qualche astrologo si serviva in Grecia a quell'epoca.
      Una lettura in chiave esoterica di tali codici, a detta degli studiosi dell'800, riserva qualche sorpresa. L'autore del testo francese fa osservare che questo sistema di notazione sembra fondato sul medesimo principio di quello dell’antica Massoneria: un medesimo modulo grafico di base variato in più modi, il cui angolo destro che raffigura la squadra – particolare interessante per i moderni Massoni – è la base, e che segue, aumentando per decine; le medesime trasmutazioni. Tale avvicinamento però, sembra indicare un'origine orientale, il che è confermato dai termini usati in proposito dagli studiosi del ‘500.

I NUMERI DEGLI ASTROLOGI CALDEI. Per gli umanisti, infatti, un tale tipo di notazione numerica riporta con poche variazioni i numeri degli antichi astrologi e dei Caldei. Johan Bronchorst, noto come Giovanni da Nimega, nel suo trattato De numeris (Parigi 1539) riporta che quelle cifre gli sono state comunicate dal dotto Rodolfo Paludanus di Nimega. Le cifre si differenziano da quelle di Pâris soprattutto in questo, che la linea di base è tracciata in orizzontale anziché in verticale. Dal canto suo, Georges Henisch, medico e matematico di genio, ha esposto nel suo trattato De numeratione (Augsburg 1605) una tavola numerica più completa e meglio disposta di quella di Giovanni da Nimega:

Sotto tale forma, come si vede, la legge interna che unisce le unità dei diversi ordini numerici appare molto più chiara. La combinazione dei tratti che rappresentano le unità, le decine, le centinaia e le migliaia permette di raffigurare ogni numero. Giovanni da Nimega dà gli esempi seguenti, relativi alla data di pubblicazione del

suo libro.Il volume del Magasin pittoresque che abbiamo casualmente ritrovato («Dix-huitième année, 1850») vorrebbe dimostrare, insomma, nel suo curioso articolo («Chiffres singuliers employés par les astrologues et attribués aux Chaldéens»), che dall'antichità fino almeno al diciassettesimo secolo non le cifre “arabe”, ma le cifre «greche», caldee o astrologiche che fossero, sono state in realtà il fondamento – oggi dimenticato o comunque poco noto – della scrittura dei numeri in tutto l’Occidente. Pur con varie e rocambolesche evoluzioni che hanno condotto i segni numerici riportati da Matthieu Páris ad incrociarsi e legarsi tra loro in una sorta di corsivo koiné d'uso corrente. Ma era davvero corrente un siffatto tipo di scrittura numerica al di fuori dei circoli chiusi degli scienziati e degli astrologi? Difficile dirlo. Ad ogni modo, a parte il carattere misterico e criptico dei numeri antichi, questa riscoperta impone una considerazione – minimalista, ma non per questo meno amara – a noi moderni lettori: le pubblicazioni a dispense del 1850, almeno a Parigi, erano sicuramente più intriganti e meno superficiali di quelle che oggi troviamo in edicola.

AGGIORNATO IL 29 LUGLIO 2016